有限元法是在现代计算机飞速发展的基础上发展起来的一种近似数值方法。用于求解力学和数学中具有特定边界条件的偏微分方程问题。这些偏微分方程是工程实践中常见的固体力学和流体力学问题的基础。

有限元和计算机的发展共同构成了现代计算力学的基础。有限元法的核心思想是“数值逼近”和“离散化”，所以它在历史上的发展也是围绕着这两点展开的。

1.数值逼近

因为在有限元方法发明之前，所有在工程问题中出现的力学问题和偏微分方程只能可以通过简单的解析解来解决。这种方法需要大量的数学运算，并且严重依赖于一些理想化的假设。例如，在土木工程的梁柱计算中，会出现平截面假设、小应变假设、理想塑性假设等。这些假设实际上与实际工程问题有很大的偏差，一旦工程问题稍微复杂一点，就不能直接得到解析解，或者解析解的误差太大。

有限元法将复杂结构离散为有限个单元，然后将这种理想化的假设和机械控制方程应用于结构然后通过单元分析和装配得到结构的总刚度方程，通过边界条件等约束求解各单元的响应，避免直接建立复杂结构的力学和数学模型。整个过程可以描述为：

总结构离散化——单元力学分析——单元装配——总结构分析——应用边界条件——获取结构单元总响应-内反应分析

单元分析和单元内反应过程中，形函数插值和高斯数值积分是用来近似表示单元内部任意一点的反应，是有限元数值逼近的重要体现。一般来说，形状函数的阶数越高，逼近精度越高，但也需要更多的单元控制点和高斯积分点。此外，单位划分得越细，近似结果就越准确。但是，上述两种提高有限元精度的代价是计算量几何倍数的增加。

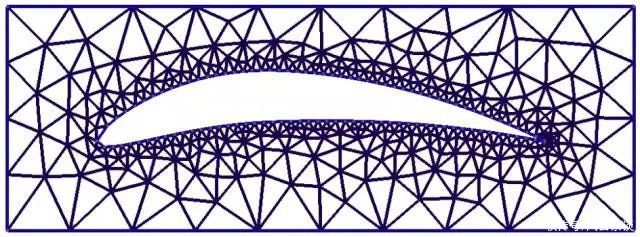
为了在最小化计算量的同时提高数值逼近的精度，有限元法经历了许多发展和改进。下图是一个典型的有限元问题。由于模型中空部分的几何不规则性，结构被有限的三角形单元分割。在外围区域，结构响应不是很大，所以划分的单元比较大，比较粗糙，而在内部，应力变化比较大，划分比较细。

在单元划分最密集的区域，存在应力集中现象，因此有相应的先进理论（如非-局部理论）来指导这部分单元的应力应变计算。结构被选择性离散化，先进的理论构成了有限元发展的主要研究方向。

2.离散化

离散化及其对应的单元特性和收敛性的研究也是有限元的一个重要研究领域。也就是说，有限元和组装在其中的整体结构主要分为：

一维单元（1- D 元素)

bar 元素------桁架

板单元------壳

二维单元------平面应力和平面应变< /p>

三角形元素)

四边形元素

多边形元素

3-D元素------三维结构（ 3-D问题）

四面体元素

六面体元素

多面体元素

具体分类及单元形状如下图：

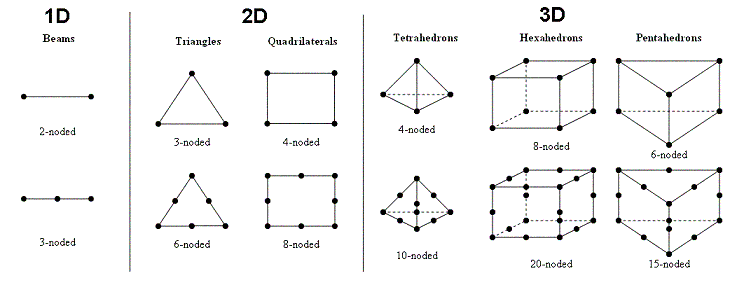
可以看出每个单元可以增加形状函数（控制点节点的数量）以提高精度。许多有限元研究也集中在这一领域。例如，研究新单元并将其应用于结构动力响应以减少数值振荡，例如使用3-D单元来模拟梁单元等。其实从理论上讲，这个领域可以有无限可能，因为对精度和数值稳定性的追求可以是无限的。

3. “平滑边界”与CAD交互 p>

其实这不是有限元的核心思想，而是有限元研究领域热火朝天的领域.它是“NURBS”有限元方法。它的原理是利用空间样条曲线来划分单位。如第一张图所示，传统的有限元处理在处理不规则边界时通常使用较多的单元，并使用三角形单元和多边形单元进行求解，并且单元的控制点都与单元在同一平面上。 NURBS单元的控制点与单元本身分离，使用B样条理论上可以在不显着增加计算量的情况下将单元的连续性提高到无穷大。

文章来源：《固体力学学报》 网址: http://www.gtlxxbzz.cn/zonghexinwen/2021/0809/663.html

上一篇：钱学森能抵五个师，美国为何仍放他回国？我国
下一篇：“诗人院士”王玉明：永怀赤子心